Содержание Показать
Одним из самых важных и фундаментальных понятий в линейной алгебре является вектор. Векторы окружают нас повсюду, хотя они часто остаются невидимыми для нас. Поэтому их обычно вводят через строгое математическое определение или обсуждают в контексте реальных примеров, таких как скорости, силы и ускорения.
Для более интуитивного и, надеюсь, быстрого понимания этого важного понятия, данный урок начинается с игры и наглядной визуализации того, что может быть вектором. В данном случае рассматривается скорость мяча, которая включает направление (куда движется мяч) и величину скорости (как быстро он туда движется):
Знакомство с вектором
Вектор имеет как геометрический, так и алгебраический смысл, и давайте разберемся с каждым из них по порядку.
Геометрический смысл
Все верно, вектор — это математический объект, который имеет две основные характеристики: длину и направление. И обычно он представляется в виде стрелки, где длина стрелки указывает величину (или длину), а направление стрелки — направление вектора - и если же изменить хоть один из этих характеристик, получится новый вектор.
И пока эти два параметра остаются неизменными, вектор обладает уникальной способностью перемещаться в пространстве, сохраняя свою идентичность.
То есть, вектор не меняется от перемещения по плоскости, значит, точно такой же вектор [math] \vec{F}[/math] можно отложить от точки (0, 0). Получаем, [math] \vec{F}=(4, 2)[/math].
Один из способов обозначения вектора — использование двух заглавных латинских букв, например [math] \vec{AB}[/math] , где точка ([math]A[/math]) является начальной точкой вектора, а точка ([math]B[/math]) — его конечной точкой.
Стрелка или черта над буквами указывает на то, что это вектор, а не просто две точки. Изменение порядка букв на [math] \vec{BA}[/math] обращает вектор, указывая на противоположное направление, что делает его совершенно другим вектором с точки зрения направления.
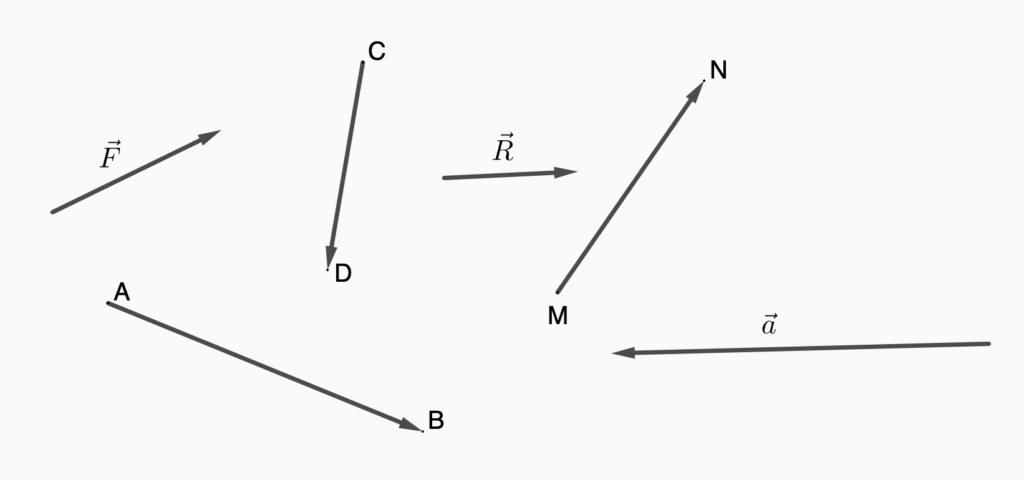
Другой способ обозначения вектора — использование одной строчной буквы, например [math]\vec{a}[/math],
с чертой или стрелкой наверху. Это представление чаще используется, когда точное начало и конец вектора не указаны или не важны, и внимание уделяется величине и направлению вектора в целом.
Однако, когда речь заходит о векторах, просто знать их длину и направление может быть недостаточно для решения реальных задач. Для того чтобы эффективно использовать векторы в решении реальных задач, необходимо разместить их в определенной системе координат. Это позволяет нам определить их точное положение в пространстве, а также упрощает выполнение операций, таких как сложение, вычитание и масштабирование векторов.
Подробнее о системах координат
Для того чтобы определить положение вектора в пространстве, необходимо ввести систему координат, то есть установить определённые правила. Существует множество различных способов задания системы координат, но одной из наиболее известных и широко используемых является декартова система координат.
Она создаётся с помощью двух взаимно перпендикулярных линий, которые называются координатными осями. Эти оси взаимно пересекаются в точке, известной как начало координат.
Для определения положения точки на плоскости в декартовой системе координат используются две координаты:
• Первая координата, называемая осью абсцисс, измеряется вдоль оси [math]Ox[/math], которая обычно горизонтальна.
• Вторая координата, называемая ось ординат, измеряется вдоль вертикальной оси [math]Oy[/math].
Каждая точка на плоскости или в пространстве может быть точно определена этими двумя числами в контексте выбранной системы координат.
Чтобы найти координату точки по оси, нужно опустить из неё перпендикуляр на эту ось.
Запишем координаты точек, изображённых на координатной плоскости $$A=(2, 5), B=(3, 2), C=(-4, 3), D=(0, 6), E=(-3, -3),$$ $$F=(-1, -1), G=(4, -4), V=(0, -4), I=(3, -1)$$
Алгебраический смысл
Если в геометрии вектор — это отрезок, указывающий направление и длину, то в алгебре вектор представлен набором чисел, называемых координатами, которые можно записать в строчку или в столбик.
Как упомянуто выше, координаты вектора можно записывать в двух основных формах: горизонтальной (строкой) и вертикальной (столбцом).
- Горизонтальная запись (строка):
- Круглые скобки: Координаты разделяются запятыми и заключаются в круглые скобки, например, [math](x, y)[/math] для двумерного пространства.
- Угловые скобки: Иногда используются для обозначения векторов, например, [math]\langle x, y \rangle[/math] .
- Вертикальная запись (столбец):
- Круглые скобки: Координаты располагаются одна под другой и заключаются в круглые скобки, например:
\begin{pmatrix} x \\ y \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} - Квадратные скобки: Аналогично предыдущему, но координаты заключены в квадратные скобки, например:
\begin{bmatrix} x \\ y\end{bmatrix}\begin{bmatrix} x \\ y \\ z \end{bmatrix}
Обе формы записи широко используются и выбор между ними часто зависит от контекста задачи и личных предпочтений.
Вектор в пространстве
До сих пор внимание было сосредоточено на векторах с двумя координатами, однако в математике и физике встречаются векторы с любым количеством координат. Каждая координата в векторе соответствует определенному измерению в пространстве.
Одномерные векторы, например, [math] \vec{M} = (7) [/math], лежат на прямой линии и имеют всего одну координату, которая указывает их положение на этой линии. Они могут представлять, например, величины в физике, такие как время или температура, где имеется только одно измерение.
Двумерные векторы уже расположены на плоскости и имеют две координаты. Это наиболее знакомый тип векторов, который часто изображается в виде стрелок на графике, где каждая координата определяет положение вектора вдоль соответствующей оси, [math]\vec{OA} = (8, 8) [/math].
Трехмерные векторы вводят еще одно измерение, добавляя третью координату. Они располагаются уже не на плоскости, а в пространстве, и их часто используют для описания физических объектов в трехмерном мире, например, в механике или архитектуре.
Аналогично, векторы могут иметь четыре и более измерений. Хотя такие векторы уже не представить графически в нашем трехмерном мире и по этой причине приходится ограничиваться трехмерными визуализациями для графического представления, а для векторов с большим числом измерений используют числовое представление, т.к. они имеют большое значение в более абстрактных областях, таких как многомерная статистика, компьютерное зрение и машинное обучение, где они могут представлять множество различных свойств или измерений объекта.
Все эти векторы, независимо от количества измерений, подчиняются общим правилам и операциям векторной алгебры, что делает их универсальным и мощным инструментом в науке и в инженерии.
В общем виде вектор можно записать так.
[math]{a_n} = (\alpha_1, \alpha_2, …, \alpha_n)[/math]
[math]{b_n} = (\beta_1, \beta_2, …, \beta_n)[/math]
В общем случае вектор в n-мерном пространстве записывается как [math]{a_n} = (\alpha_1, \alpha_2, …, \alpha_n)[/math], где каждая координата представляет собой величину вектора вдоль одной из осей многомерного пространства. В математических записях для обозначения координат часто используются греческие буквы, такие как альфа (α) для первой координаты, бета (β) для второй, гамма (γ) для третьей и так далее, придавая формулам универсальность и международное понимание.
Греческие буквы
| Буква | Название | Буква | Название |
|---|---|---|---|
| α | альфа | ι | йота |
| β | бета | κ | каппа |
| γ | гамма | λ | лямбда |
| δ | дельта | μ | мю (ми) |
| ε | эпсилон | ν | ню (ни) |
| ζ | дзета | ξ | кси |
| η | ита (эта) | ο | омикрон |
| θ | тета | π | пи |
| ρ | ро | σ | сигма |
| τ | тау | υ | ипсилон |
| φ | фи | χ | хи |
| ψ | пси | ω | омега |
Равенство векторов
В начале статьи было упомянуто, что любой вектор определяется двумя ключевыми характеристиками: его длиной и направлением. Теперь давайте более внимательно рассмотрим концепцию длины вектора.
Длина вектора [math]\overrightarrow{AB}[/math] равна длине отрезка [math]AB[/math]. Это обозначается как [math]|\overrightarrow{AB}|[/math]. Длина вектора всегда является положительным числом или нулём. Нулевая длина возникает в случае, когда начало и конец вектора совпадают, образуя так называемый нулевой вектор, который по сути представляет собой точку. Так, любая точка на плоскости может быть рассмотрена как нулевой вектор с координатами [math](0, 0)[/math] .
Длина вектора представляет собой числовое значение, позволяющее сравнивать векторы между собой по величине. В геометрическом контексте два вектора считаются равными, если они имеют одинаковое направление и длину. Однако, на практике определять равенство векторов "на глаз" неэффективно и неточно.
В линейной алгебре для сравнения векторов используется более точный алгебраический подход. Согласно ему, два вектора [math]\vec{a} = (a_1, a_2, …, a_n)[/math] и [math]\vec{b} = (b_1, b_2, …, b_n)[/math] считаются равными, если все их соответствующие координаты равны друг другу. Иными словами, вектора равны, если выполнено условие: для всех [math]i[/math] от 1 до [math]n[/math], [math]a_i = b_i[/math].
Этот метод сравнения векторов позволяет точно определить, равны ли они, сравнивая их координаты поэлементно. Такой подход широко используется в математике и её приложениях, где требуется точность и строгость определений.

 помощник
помощник